文档库
论文阅读笔记
AutoAttack

AutoAttack

笔记作者：BrickLoo

Reliable Evaluation of Adversarial Robustness with an Ensemble of Diverse Parameter-free Attacks
Francesco Croce, Matthias Hein
Proceedings of the 37th International Conference on Machine Learning, PMLR 119:2206-2216, 2020.

Publisher   GitHub   arXiv   Semantic Scholar

简介

意义

为模型鲁棒性提供更规范化的评估方式。// 另一方面来说改进了 PGD 攻击，攻击性更强

背景

最普遍的评估方法是使用 PGD 攻击。然而——

  • 一方面，PGD 有较多超参数需要调整；// 比较不公平
  • 另一方面，PGD 本身也不一定能保证成功率（作者认为可能的原因在于 PGD 的固定步长，以及损失函数的选择问题），导致性能高估；// 固定的步长如果选择不当可能不收敛并影响性能
  • PGD 的迭代次数具有误导性，攻击的损失值在数次迭代后趋于稳定，攻击效果不会随着攻击的预算（即循环次数）的增加而显著增加；// 也是固定步长的选择问题
  • 此外，作者认为评估过程应该提高攻击方式的多样性；

改进思路

提出两种 PGD 变体来分别解决问题（其中“迭代次数”是唯一的超参数），并结合两个同期工作中提出的攻击方法（白盒 FAB 攻击和黑盒 Square 攻击），综合评估模型鲁棒性。

文章的创新点在于，

  • 提出了无需调参的 APGD 方法，整个算法流程的设计有很多亮点；
  • 提出 DLR 损失来提高攻击稳定性；
  • 结合多种攻击方法进行评估，保守估计模型鲁棒性；

实验思路

选取 35 篇论文中的 50 个鲁棒模型进行评估。

APGD (Auto-PGD)

改进

  • 步长以先大后小的规律进行调整
    • 大步长时为了避免方向受到局部梯度信息影响而剧烈变化，加入动量机制；
  • 每过一段间隔设置一个检查点，根据损失变化趋势来判断是否应该调整步长，当优化速度放缓时尝试减小步长让其更好收敛
    • 按照比例而非迭代次数来设置检查点；// 主要是为了照顾迭代次数比较少的攻击
    • 作者认为越迭代收敛应该越快，间隔应该要逐步减小；// 在局部搜索最优解相对更简单
    • 在检查点时根据条件检查是否需要减小步长
      • 条件 1：检查点之间，如果成功优化的次数少于一定比例，则减小步长
        • 成功优化的比例可以反映优化速度；
        • 考虑极端情况，算法可能会让对抗样本在某一个位置徘徊，陷入循环；
      • 条件 2：如果与上一次检查点相比，步长没有改变，最佳对抗样本也没有改变，则减小步长
        • 这个条件是用来完善另一个条件中的循环问题；
    • 减小步长的同时将对抗样本恢复至最优情况，继续在附近搜索；

超参数选择

  • 初始步长：$2\epsilon$
  • 步长减小的比例：$0.5$
  • 动量参数：本轮影响力 $0.75$，上一轮影响力 $0.25$
  • 检查点选取方式：第 $\lceil p_j N_{iter} \rceil$ 个循环为检查点，其中 $p_0 = 0$， $p_1 = 0.22$， $p_{j+1} = p_j + max \lbrace p_j-p_{j-1}-0.03,0.06 \rbrace$
  • 成功优化比例的阈值：$0.75$

步骤

APGD 算法伪代码 解读：

  • 3 行：初始化
  • 4 - 5 行：比较并保存最优对抗样本
  • 6 - 17 行：迭代搜索更优的对抗样本
    • 7 - 8 行：应用动量机制生成新的对抗样本
    • 9 - 11 行：备份最优对抗样本
    • 12 - 16 行：判断当前轮是否为检查点，并进行相应操作
      • 13 - 15 行：判断是否应该减半步长
        • 14 行：步长减半并继续在最优对抗样本附近搜索

实验

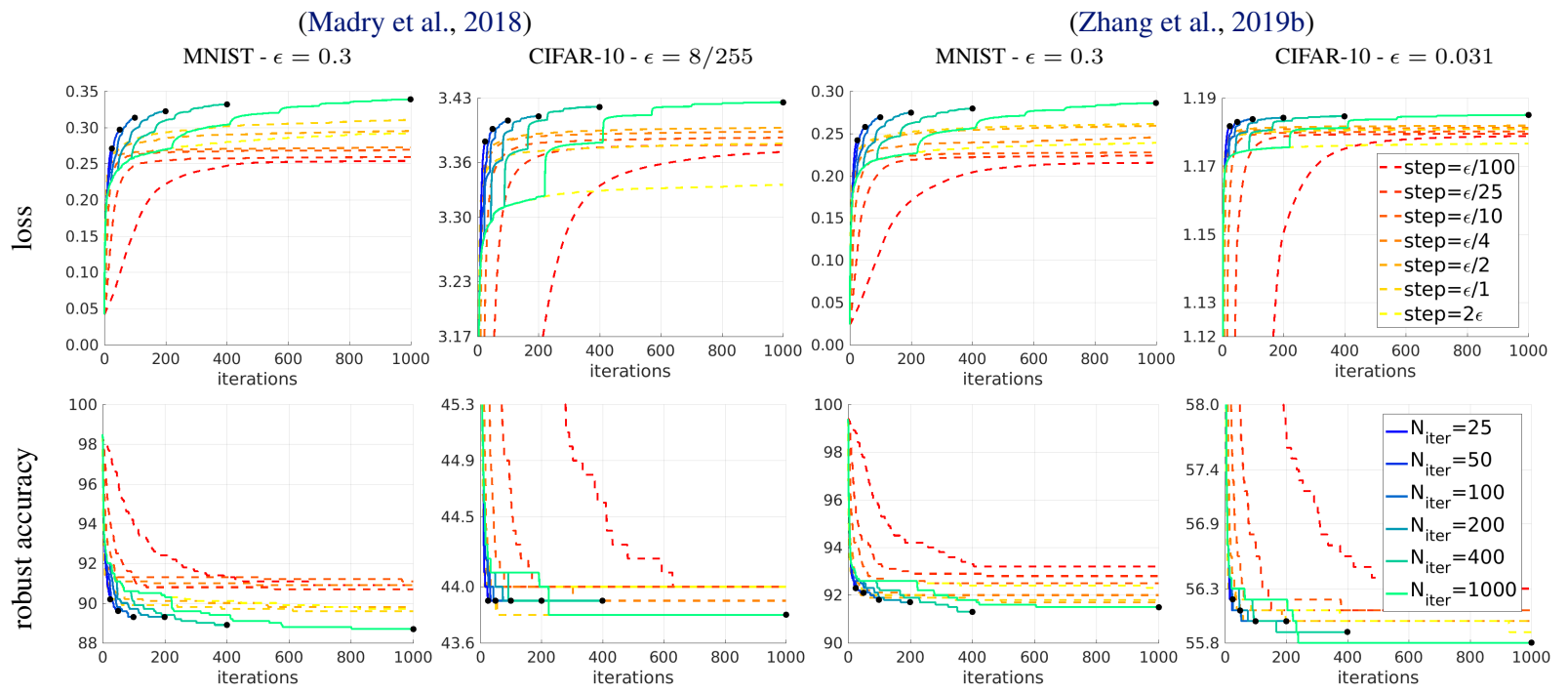
实验对比 APGD 与运用了动量的 PGD
图中虚线为应用动量机制的 PGD，实线为作者提出的 APGD；
图中比较值得注意的点是，

  • 应用动量的 PGD 并非步长越小越好，超参数的选取会影响攻击效果；
  • 不同场景下的最优步长可能不同；
  • 迭代次数较多时 APGD 会搜索得更慢，但是最终效果更好；
  • 迭代次数较少时 APGD 在不用选择参数的情况下攻击效果也还算不错；

DLR (Difference of Logits Ratio)

背景

PGD 攻击方法的迭代中需要用到损失函数的梯度信息来搜索对抗样本。前面提到作者认为损失函数的选择是 PGD 无法保证攻击成功率的原因之一。

理论论证

常用的损失函数是 CE（交叉熵）损失 $$CE(x,y)=-\mathop{log}p_y=-z_y+\mathop{log}(\sum\limits_{j=1}^K e^{z_j})$$ 其中，$z$ 是 logits 值，$p_i = e^{z_i} / \sum_{j=1}^K e^{z_j},\ i=1,…,K$
CE 损失只具有平移不变性，但是不具有缩放不变性。// 不太确定平移不变性的部分，但是作者认为缩放不变性是罪魁祸首

继续对 CE 求导，我们可以得到 $$\nabla_x CE(x,y)=-\nabla_x z_y+\frac{\sum_{i=1}^K e^{z_i} \nabla_x z_i}{\sum_{j=1}^K e^{z_j}}=(-1+p_y)\nabla_x z_y + \sum\limits_{i \neq y}p_i \nabla_x z_i$$ 在正确预测时，概率最大的类别为正确的类别 $y$。如果预测得分 $z_y$ 与其他类别 $x_i$ 差得很多，那么计算出来的 $p_y$ 则可能趋近于 $1$，其他类别 $p_i$ 趋近于 $0$，使得整个 CE 损失的导数趋近于 $0$，甚至在计算机的精度下等于 $0$，导致其无法被 PGD 用以迭代改进。这种现象在 C&W 攻击方法的论文中被发现。

而在白盒攻击中，攻击者可以对 logits 值进行缩放，避免梯度消失的问题，进而能够通过 PGD 生成有效的对抗样本。如果评估鲁棒性时未考虑这一因素，则会导致模型性能的高估。

实验论证

作者同时做了实验进行验证：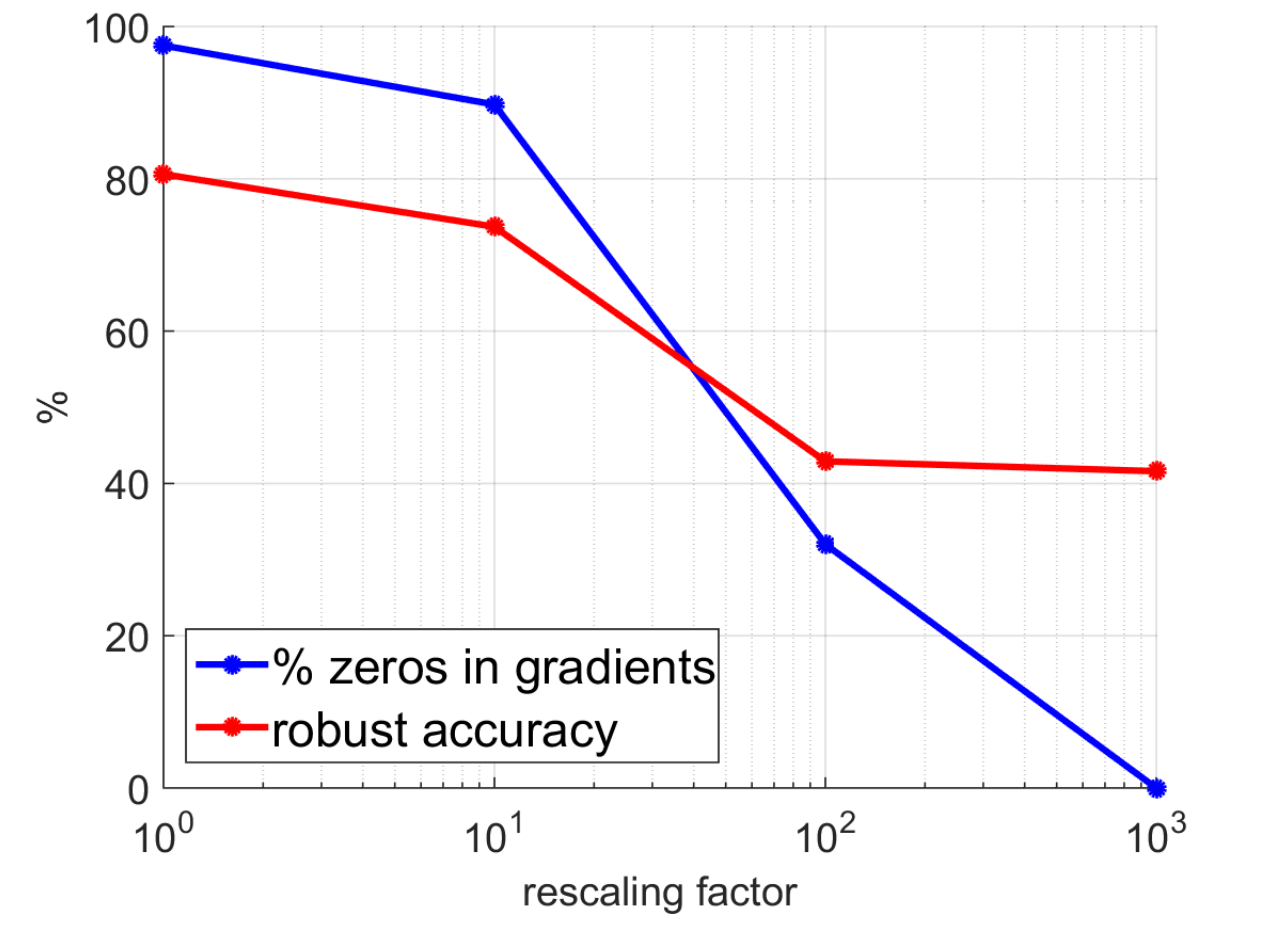
CE 损失的梯度消失实验
图中横轴表示对 logits 值进行缩放的操作中，分母选取的大小； 图中比较值得注意的点是，

  • 当不缩放 logits 时，梯度信息几乎全部消失；
  • 对 logits 进行缩放后，模型鲁棒性显著变差，说明实验中如果没有考虑这个因素会导致鲁棒性高估；

改进

作者基于 C&W 中选取的损失函数 $CW(x,y)=-z_y+\mathop{max}\limits_{i \neq y}\lbrace z_i\rbrace$ 进行改进（因为这个损失函数求导后依然受到 logits 值本身的数值大小影响，不具有缩放不变性）

作者提出的替代损失函数名为 DLR $$DLR(x,y)=-\frac{z_y-\mathop{max}\limits_{i \neq y}\lbrace z_i\rbrace}{z_{\pi_1}-z_{\pi_3}}$$ 式中，$z$ 是 logits 值，$\pi$ 及其下标表示降序排序中的位次信息。由于最大得分的错误类别只可能处于第一或第二的位次，作者通过第一位次和第三位次的分差作为分母，使得最终的损失值落在 $(-1,1)$ 之间。如果对 logits 值进行缩放，DLR 会产生抵消，维持缩放不变性，保证其自由度与分类器的决策相等。

同时，作者也为针对性攻击场景设计了替代损失函数 Targeted-DLR $$Targeted\text{-}DLR(x,y)=-\frac{z_y-z_t}{z_{\pi_1}-(z_{\pi_3}+z_{\pi_4})/2}$$ 可以看到分母发生了变化。这是为了避免目标位次恰好处于第三位时，损失函数恒为 $1$，进而梯度恒为 $0$，导致无法优化对抗样本。

实验

作者进一步将不同损失函数的 APGD 与 PGD / 带动量机制的 PGD 进行对比，并尝试了包括 $L_\infty$ 和 $L_2$ 范数限制的攻击场景；// 这部分的实验数据不放了，感兴趣可以查看原论文
得出的结论是，

  • APGD 的攻击性能优于 PGD / 带动量机制的 PGD；
  • DLR 损失相比于 CE 损失，攻击效果相对更好；
  • DLR 损失相比于 C&W 损失，攻击效果差距不大，但 DLR 的表现更加稳定；

AutoAttack

除了 APGDCE 和 APGDDLR 两个版本的攻击方式，作者将另外两个同期工作中的无参数攻击（白盒 FAB 攻击和黑盒 Square 攻击）也打包在一起，用作综合评估。

FAB 攻击简介

这种攻击方法会尽可能地减小扰动范数；
虽然该方法依赖于 logits 的梯度，但是对于应用了梯度掩蔽防御的模型似乎也有效果；

Square 攻击简介

这种攻击方法是基于分数的黑盒攻击；
该方法使用随机搜索，不使用梯度信息；

评估规则

作者的评估规则是使用四种方法分别生成对抗样本，除非没有一种方法攻击成功，否则将这个样本记为攻击成功。最后计算攻击成功率作为评估结果。// 个人感觉，其实要攻击者每一种方案都尝试的话不是很合理，或许直接选择评估情况最差的攻击方法作为最终的评估结果还合理一些……但是安全起见选择保守估计也可以理解，而且数值上差别不大

对于随机化防御的模型，作者的策略是应用 Expectation over Transformation 思想，对每一次迭代执行 20 次重复的梯度计算以求出合理的梯度均值。然后将 AutoAttack 整体运行 5 次，取平均值作为评估结果。作者同时给出了方差信息，但是方差相对较小，四舍五入基本没有影响，可以说明这个成绩是对于随机化防御的模型是比较合理的。

论文阅读笔记